Welcome to Order in Entropy

Well, first thing’s first. The name of this blog comes from the most common explanation of Entropy, which goes like “Entropy means disorder”, or “Entropy causes disorder”, etc., there are many variants.

This blog is to better my understanding of nature and its secrets; and I hope I can be of some help to those who have similar interests.

Back to entropy, it is not precisely a measure of disorder. It is a measure of how much energy is spread out, or diffused into the surrounding region from a point of interest. If energy spreads out from a point in space (think of a gas expanding), change in entropy of the process is positive. If energy contracts and gets clumped up into a region of space (imagine clumping up a spread out piece of clay into a ball), then the change in entropy is negative. If there is no spread in the energy, the process has zero change in entropy.
So, we can say that entropy is directly proportional to the amount of energy, or heat in a system.
We do not make much use of entropy in itself, but the change in entropy is what we need to look at. Entropy in itself tells us about the number of configurations of each particle in a system. Each of these configurations is called Microstate. More the entropy, more the number of configurations of the particles, the more ‘random’ the state is. A change in entropy tells us how much change is there in the number of microstates, or how much randomisation has happened in the system.

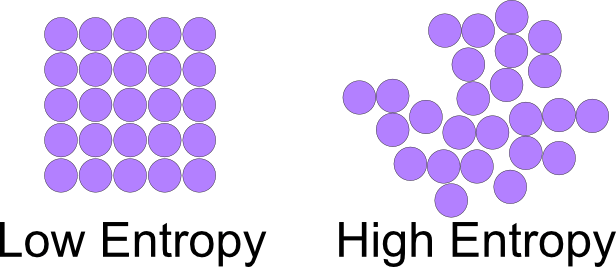
According to this picture, we can see that there are only a few microstates in which the particles are bonded and static. But there’s a large number of microstates in which the particles are free and moving, by courtesy of its position!

Each particle can be at any place, thus the combinations of all particles at each position in a system is much much higher than the configurations in which all the particles are stuck, clumped or bonded with each other in a tight space. Out of all the space, if the particles assemble into a fixed rigid construct, they have limited freedom to go wherever they want. In this case they have fixed positions.

If you consider the first pic and look at space like a grid of positions, or a matrix, one particle can be present at any of the 25 positions only out of, maybe, hundreds of thousands of positions in space. There has to be some force keeping them together.

The 2nd pic shows the particles in random locations. This means they can take up any of the positions in space. The probability of finding a group of particles clumped together without any force keeping them so, is thus, very less. The number of situations where they come together automatically is so less, that’s why nature likes disorder better.

Let’s take a cup of tea or coffee, whatever you like.
We all know how to cool it if it’s too hot. Yeah, you guessed it. Pour it from one cup into another cup from a height! In fact there are many tea shops, where I’ve seen the tea sellers expertly pouring tea from one cup to another from great heights.
Try this at home. Take a cup of any hot drink, take another empty cup, pour it from a small height and very slowly. Try drinking it. Nope, it’s too hot right? Now pour the same drink from a much greater height suddenly into the other cup. Suddenly it’s not that hot, huh?
NOTE: This requires expertise and the first few times, I poured the tea all over myself and some other strangers, from whom I had to run. So do this at your own risk 😛

Basically, when you pour the drink suddenly while there’s a high distance between the cups, the change of the configuration of the drink particles is sudden and irreversible. There is no way to bring back the exact configuration of the particles; well in actuality, the probability of the drink particles retaining their exact same position while transitioning between two cups is so small, we say it’s zero. This, is an example of an Irreversible process.

Each time the drink is poured, the configuration is randomised repeatedly. The particles gain and lose energy, courtesy of the average heat of the drink and the gravitational energy we provide by lifting the cups in the air. While the gravitational energy is changeable, i.e. can be increased and decreased by changing the position of the cups, the thermal energy can not be increased unless you heat it, and well, that’s just stupid ’cause we’re trying to drink the damn drink and it’s too hot already. Who in their right mind would heat up an already hot drink? Anyway, the heat from the cup dissipates while poured from one cup to the other because when the drink particles collide with air molecules, the latter absorbs a lot of energy and gets excited, while the former cools down and falls into the other cup. And since air is a gas, it’s tougher for all that energy to get clumped back together and go back into the drink because that process involves the configurations of gas particles that are like, one in a million. Gas particles are already excited and move about rapidly from ambient heat and the energy they gained from the drink just energised them more to escape away. The probability of the gas giving back the energy it gained from the drink particles is so low, that it just doesn’t happen.

So well, nature follows probability.

Each step in this process of pouring the drink heats up the surrounding air and the heat energy is lost. Now, don’t test whether the air has turned to steam or something, lol. The energy lost is not that high, hence we have to repeat this again and again until an equilibrium i.e. a balance is achieved between the temperature of the drink and its surroundings.

Thus change in entropy in this process is positive, and the number of microstates has increased as there are more configurations the gas particles can take with the energy they gained from the drink particles. Although the number of configurations the drink particles can take is decreased due to lesser energy to move due to loss of heat to the gas particles, the net change in the number of microstates is positive, because the gas particles are already more random, i.e. they already can move freely amongst each other. Hence they can take up a lot more number of microstates than the drink particles.

When we try pouring the drink between cups slowly and from a very short distance in height, there is very less loss of heat. Why, you ask?
There isn’t much space for the heat to dissipate into the air between the cups, and since the change happens very slowly, we can say the configurations of the particles can be retained. Although, in this example, that doesn’t happen, in processes or reactions that happen very slowly, by slow I mean millions of years- slow, the configurations of the position of each particle does not change much, hence there is very less diffusion of energy into the surroundings. Hence the entropy in this process is approximately zero. This kind of a process is called a Reversible process, one in which you just can’t see the change happening. Without a watch, and without a way to tell time, by looking at the microstates of the particles, you just can’t determine the change in entropy.

Entropy is represented by S, and its change by ΔS.

All processes in reality are Irreversible in nature, and some take extremely long time, so we approximate them as Reversible.

Thus, in reality, ΔS ≥ 0.

Entropy of the universe is always increasing, in hopes that all of heat becomes uniform and that it comes to an equilibrium.

This is bad for us, as we require heat from the Sun to live and equilibrium here means that the Sun doesn’t produce heat of its own.
Fortunately, the universe still has a long way to come to an equilibrium and we’d be long gone by that time, anyway.

We’re just another spec in the vast empty expanding space and all this will end in a slow death.

Or will it?